SciPy - signal.remez() Function

scipy.signal.remez() is a function in SciPy's signal processing module that designs optimal Finite Impulse Response (FIR) filters using the Parks-McClellan algorithm. This method minimizes the maximum error between the desired and actual frequency responses which resulting in an equiripple filter.

This function is useful for designing low-pass, high-pass, band-pass and band-stop filters with precise control over the passband and stopband characteristics.

Syntax

The syntax for the scipy.signal.remez() function is as follows −

scipy.signal.remez(numtaps, bands, desired, weight=None, Hz=None, type='bandpass', maxiter=25, grid_density=16)

Parameters

Here are the parameters of the scipy.signal.remez() function used for designing FIR filters −

• numtaps: The number of filter coefficients (taps). Must be an odd number.
• bands: A sequence specifying the frequency bands. Frequencies should be in increasing order.
• desired: A sequence specifying the desired gain in each frequency band.
• weight (optional): A sequence of weights applied to each band to control the approximation error.
• Hz (optional): Sampling frequency in Hz. Default value is None which assumes the Nyquist frequency is 1.
• type (optional): The type of filter, either 'bandpass', 'differentiator' or 'hilbert'. Default value is 'bandpass'.
• maxiter (optional): The maximum number of iterations during optimization. Default value is 25.
• grid_density (optional): The density of the frequency grid used for optimization. Default value is 16.

Return Value

The scipy.signal.remez() function returns a 1D array of FIR filter coefficients that can be used for filtering.

Designing a Low-Pass Filter

A low-pass filter allows low-frequency signals to pass while attenuating higher frequencies. It is commonly used to remove high-frequency noise from a signal. The scipy.signal.remez() function provides an efficient way to design such filters using the Parks-McClellan algorithm.

Here is an example of designing a low-pass FIR filter using the scipy.signal.remez() function −

import numpy as np
from scipy.signal import remez, freqz
import matplotlib.pyplot as plt

# Define sampling frequency
fs = 2.0  # Sampling frequency

# Design a low-pass filter
numtaps = 51
bands = [0, 0.3, 0.4, 1.0]  # Normalized frequencies (0 to fs/2)
desired = [1, 0]  # Passband and stopband gains

# Design FIR filter with explicit fs parameter
coefficients = remez(numtaps, bands, desired, fs=fs)

# Frequency response
w, h = freqz(coefficients, worN=8000, fs=fs)

# Plot the frequency response
plt.plot(w, 20 * np.log10(abs(h)))
plt.title('Low-Pass Filter Frequency Response')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude (dB)')
plt.grid()
plt.show()

Below is the output of designing a low-pass filter using scipy.signal.remez() function −

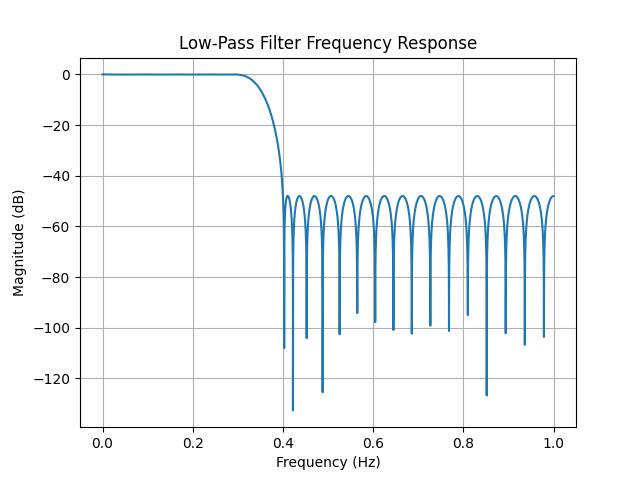
Designing a Band-Pass Filter

A band-pass filter allows frequencies within a specified range to pass while attenuating frequencies outside the range. Here is an example of designing a band-pass FIR filter using scipy.signal.remez() function −

import numpy as np
from scipy.signal import remez, freqz
import matplotlib.pyplot as plt

# Parameters
numtaps = 51
fs = 2.0  # Sampling frequency (normalize between 0 and fs/2)
bands = [0, 0.2, 0.3, 0.6, 0.7, 1.0]  # Normalized frequencies
desired = [0, 1, 0]  # Stopband, passband, stopband

# Design the band-pass filter with the specified sampling frequency
coefficients = remez(numtaps, bands, desired, fs=fs)

# Frequency response
w, h = freqz(coefficients, worN=8000, fs=fs)

# Plot the frequency response
plt.plot(w, 20 * np.log10(abs(h)))
plt.title('Band-Pass Filter Frequency Response')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude (dB)')
plt.grid()
plt.show()

Following is the output of designing a band-pass filter using scipy.signal.remez() function −

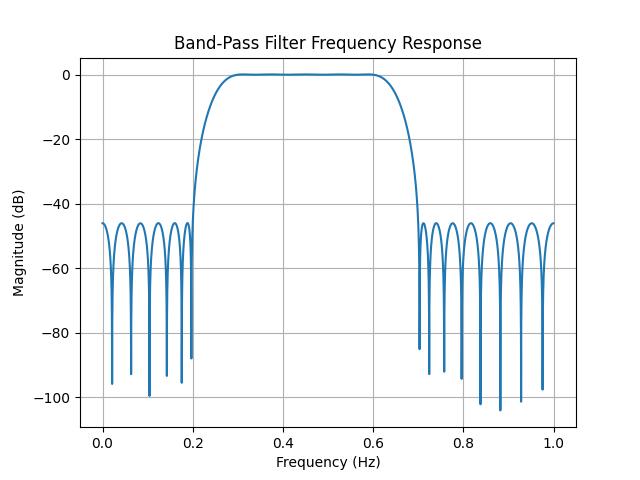
Designing a High-Pass Filter

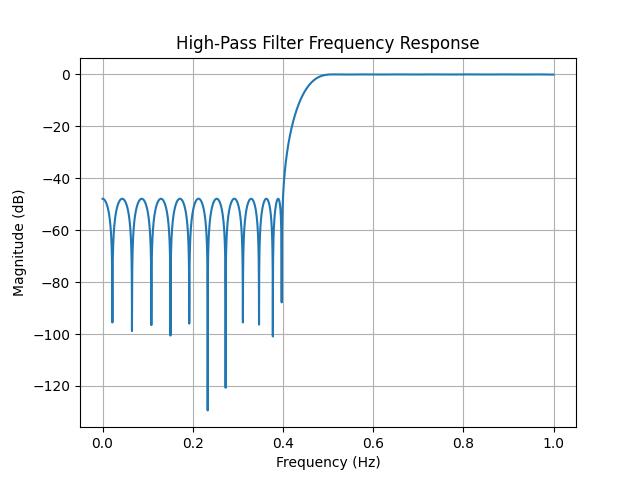
A high-pass filter allows frequencies above a specified cutoff frequency to pass while attenuating frequencies below. Here is an example of designing a high-pass FIR filter using scipy.signal.remez() function −

import numpy as np
from scipy.signal import remez, freqz
import matplotlib.pyplot as plt

# Parameters
numtaps = 51  # Number of filter taps (coefficients)
fs = 2.0      # Sampling frequency (normalize between 0 and fs/2)
bands = [0, 0.4, 0.5, 1.0]  # Normalized band edges (relative to Nyquist)
desired = [0, 1]  # Desired gain for stopband (0) and passband (1)

# Design the high-pass filter
coefficients = remez(numtaps, bands, desired, fs=fs)

# Frequency response
w, h = freqz(coefficients, worN=8000, fs=fs)

# Plot the frequency response
plt.plot(w, 20 * np.log10(abs(h)))
plt.title('High-Pass Filter Frequency Response')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude (dB)')
plt.grid()
plt.show()

Here is the output of designing a high-pass filter using scipy.signal.remez() function −